Relative entropy, KL-divergence
Entropy가 랜덤변수의 불확실성 정도를 나타내고, Relative entropy 또는 Kullback-Leibler (KL) divergence는 두 분포(distributions)의 거리를 측정하는데 쓰인다.
같은 alphabet에 대해 두 분포 p,q가 있다고 했을 때, 아래와 같이 정의한다.
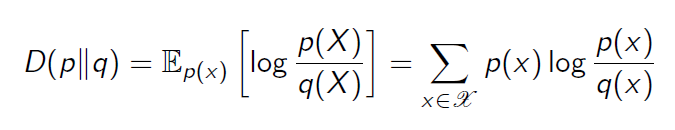
교환법칙은 성립하지 않으며($D\left(p\|q\right)\not= D\left(q\|p\right)$), 통계학에서는 distribution q의 실제 distribution이 t일 때, $D(p||q)$가 비효율성(inefficiency)의 측정으로 쓰이기도 한다.
Conditional relative entropy
Conditional relative entropy($D\left(p\left(y|x\right)\|q\left(y|x\right)\right)$)는 $p\left(x\right)$에 대한 $p\left(y|x\right)$와 $q\left(y|x\right)$ relative entropy의 기대값이다.
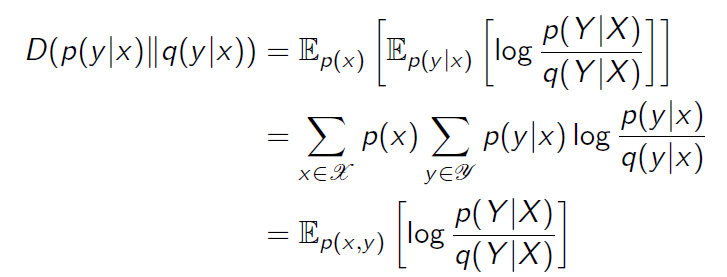
Chain rule도 성립한다.
$D\left(p\left(y|x\right)\|q\left(y|x\right)\right)=D\left(p\left(x\right)\|q\left(x\right)\right)+D\left(p\left(y|x\right)\|q\left(y|x\right)\right)$
증명)
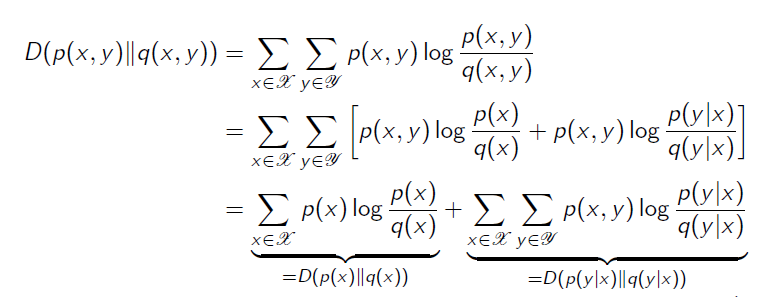
Mutual information
$\left(X,Y\right)$ ~ $p_{X,Y} \left(X,Y\right)$이고 $X$ ~ $p_X \left(X\right)\;$, 그리고 $Y$ ~ $p_Y \left(Y\right)$일 때 X와 Y의 mutual information은 X,Y의 relative entropy이다.
Mutual information은 하나의 random variable이 다른 random variable을 포함하는 정보의 평균적인 양을 나타낸다.
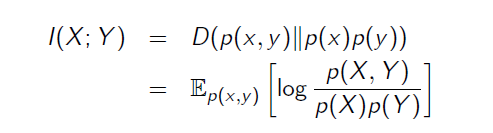
'Information theory' 카테고리의 다른 글
| JPEG Compression - JPEG압축, DCT이산 코사인 변환 (1) | 2021.05.01 |
|---|---|
| Differential entropy (0) | 2021.04.24 |
| Lossy coding과 Entropy,Distortion (0) | 2021.04.24 |
| color space transform, chroma subsampling - 색공간 변환, 크로마 서브 샘플링 (0) | 2021.04.20 |
| Memoryless source, Markov source Entropy (0) | 2021.03.02 |



