Differential entropy
이산값을 가지는 Source가 아닌, Continuous value(연속적인 값)을 가지는 Source X가 있다고 가정해보자. X는 Memoryless source이고 확률 질량 함수 pdf는 $f_x \left(x\right)$로 표기한다. 여기서 Memoryless source란 이전 값에 의존하지 않고 독립적이라는 뜻이다.
$f_x \left(x\right)$가 연속적이고, 각각의 i에 대해 $x_i \in \lbrack \left(i-1\right)\Delta ,i\Delta \lbrack ,i\in Z$이 존재한다고 했을 때, 평균값 정리(Mean value theorem)에 의해 $f_x \left(x_i \right)$는 다음과 같이 나타낼 수 있다.
$f_x \left(x_i \right)=\int_{\left(i-1\right)\Delta }^{i\Delta } f_x \left(x\right)\mathrm{dx}$
연속 값을 가지는 Source의 X를 이산화(Discritized)한 값을 $X_d$라고 정의하자. 또한 이렇게 이산 소스의 확률이 연속 소스의 확률과 같다고 가정해보자. ($f_x \left(x\right)$는 pdf이기에, 함수값과 $\Delta$를 곱해준 면적이 확률이 된다)
$X\left(\mathrm{continuous}\;\mathrm{value}\right)\to X_d \left(\mathrm{discritized}\;\mathrm{value}\right)$
$P_r \left(x_d =x_i \right)=f_x \left(x_i \right)\cdot \Delta$
$X_d$의 Entropy 는?
$H\left(X_d \right)=-\sum_{i=-\infty }^{\infty } P_r \left(X_d =X_i \right){\mathrm{log}}_2 \left(X_d =X_i \right)$
$=-\sum_i f_x \left(x_i \right)\Delta {\mathrm{log}}_2 \left(f_x \left(x_i \right)\cdot \Delta \right)$
$=-\sum_i f_x \left(x_i \right)\Delta {\mathrm{log}}_2 \left(f_x \left(x_i \right)\right)-\sum_i P_r \left(X_d =X_i \right){\mathrm{log}}_2 \Delta$
$=-\sum_i f_x \left(x_i \right)\Delta {\mathrm{log}}_2 \left(f_x \left(x_i \right)\right)-{\mathrm{log}}_2 \Delta \sum_i P_r \left(X_d =X_i \right)$
(\sum_i P_r \left(X_d =X_i \right)=1)
$\Delta \to 0$ 일 때, $\underset{\Delta \to 0}{\mathrm{lim}} \;-{\mathrm{log}}_2 \Delta =\infty$이기에 Continuous source는 무한한(INFINITE) Entropy를 가진다고 할 수 있다.
Differential entropy :
$h\left(x\right)=-\int_{-\infty }^{+\infty } f_x \left(x\right){\mathrm{log}}_2 f_x \left(x\right)\mathrm{dx}\;\;,\left(\frac{\mathrm{bits}}{\mathrm{symbols}}\right)$
원래 Entropy는 0보다 크거나 같은 양수 값만 가지지만, Differential entropy는 양수 값, 음수 값 모두 가진다.
예제) X가 [0,a]에서 Uniform distribution이라고 할 때 differential entropy인 h(x)는?
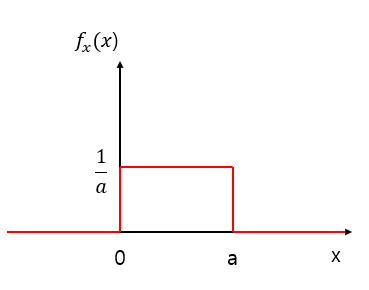
$h\left(x\right)=-\int_0^a \frac{1}{a}{\mathrm{log}}_2 \frac{1}{a}\mathrm{dx}=-{\left\lbrack \frac{x}{a}{\mathrm{log}}_2 \frac{1}{a}\right\rbrack }_0^a ={\mathrm{log}}_2 a$
a>1일 경우엔 h(x) >0
a<=1일 경우엔 h(x)<0이다.
예제)Source X가 Gaussian 분포를 따르고 평균,분산($\mu \;,\sigma^2$) 의 값을 가진다고 하자. 이 때 Differential entropy의 값이 $h\left(x\right)=\frac{1}{2}{\mathrm{log}}_2 \left(2\pi e\sigma^2 \right)$임을 보여라. (여기서 e는 Euler number이다. 약 2.71인 자연상수 e)
가우시안 분포의 pdf는 다음과 같다.
$f_x \left(x\right)=\frac{1}{\sqrt{2\pi \sigma^2 }}e^{-\frac{{\left(x-\mu \right)}^2 }{2\sigma^2 }}$
$h\left(x\right)=-\int_{-\infty }^{\infty } f_x \left(x\right){\mathrm{log}}_2 \left(f_x \left(x\right)\right)\mathrm{dx}=-\int_{-\infty }^{\infty } f_x \left(x\right){\mathrm{log}}_2 \left(\frac{1}{\sqrt{2\pi \sigma^2 }}e^{-\frac{{\left(x-\mu \right)}^2 }{2\sigma^2 }} \right)\mathrm{dx}$
$=-\int_{-\infty }^{\infty } f_x \left(x\right)\left(\left({\mathrm{log}}_2 \left(\frac{1}{\sqrt{2\pi \sigma^2 }}\right)\right)+{\mathrm{log}}_2 \left(e^{-\frac{{\left(x-\mu \right)}^2 }{2\sigma^2 }} \right)\right)\mathrm{dx}$
$=-\int_{-\infty }^{\infty } f_x \left(x\right){\mathrm{log}}_2 \left(\frac{1}{\sqrt{2\pi \sigma^2 }}\right)\mathrm{dx}+\int_{-\infty }^{\infty } f_x \left(x\right){\mathrm{log}}_2 \left(e^{\frac{{\left(x-\mu \right)}^2 }{2\sigma^2 }} \right)\mathrm{dx}$
$=\frac{1}{2}{\mathrm{log}}_2 \left(2\pi \sigma^2 \right)\int_{-\infty }^{\infty } f_x \left(x\right)\mathrm{dx}+\int_{-\infty }^{\infty } f_x \left(x\right){\mathrm{log}}_2 \left(e\right)\cdot \frac{{-\left(x-\mu \right)}^2 }{2\sigma^2 }\mathrm{dx}$
$=\frac{1}{2}{\mathrm{log}}_2 \left(2\pi \sigma^2 \right)\int_{-\infty }^{\infty } f_x \left(x\right)\mathrm{dx}+\frac{{\mathrm{log}}_2 \left(e\right)}{2\sigma^2 }\int_{-\infty }^{\infty } {\left(x-\mu \right)}^2 f_x \left(x\right)\mathrm{dx}$
$=\frac{1}{2}{\mathrm{log}}_2 \left(2\pi \sigma^2 \right)+\frac{{\mathrm{log}}_2 \left(e\right)}{2\sigma^2 }\sigma^2 =\frac{1}{2}{\mathrm{log}}_2 \left(2\pi e\sigma^2 \right)$
따라서, $h\left(x\right)=\frac{1}{2}{\mathrm{log}}_2 \left(2\pi e\sigma^2 \right)$ 이다.
평균과 분산 값을 $\mu \;,\sigma^2$ 로 가지는 Source들 중에서, Gaussian 분포는 Differential entropy를 Maximize한다. 아주 중요한 개념!X를 Gaussian 분포, Y를 Non Gaussian 분포라고 했을 때, 다음과 같은 관계가 성립한다.
$h\left(Y\right)\le h\left(X\right)\le \frac{1}{2}{\mathrm{log}}_2 \left(2\pi e\sigma^2 \right)$
Mutual information of Continuous source
Continuous value를 가지는 Source X,Y가 있다고 할 때, $X_d ,Y_d$로 이산화(Discritized) 가능하다고 하자.이 때 Conditional entropy는 아래와 같으며, Finite하다.
$H\left(X_d |Y_d \right)=-\sum_i \sum_j \left\lbrack f_{x|y} \left(x_i |y_j \right)f_x \left(y_j \right){\mathrm{log}}_2 f_{x|y} \left(x_i |y_j \right)\right\rbrack \cdot \Delta \cdot \Delta -{\mathrm{log}}_2 \Delta$
Differential entropy :
$h\left(x|y\right)=-\int_{-\infty }^{\infty } \int_{-\infty }^{\infty } f_{\mathrm{xy}} \left(x,y\right){\mathrm{log}}_2 f_{x|y} \left(x|y\right)\mathrm{dxdy}$
Mutual information은 다음과 같다.
$I\left(X_d ;Y_d \right)=H\left(X_d \right)-H\left(X_d |Y_d \right)$
$=-\sum_i f_x \left(x_i \right){\mathrm{log}}_2 \left(f_x \left(x_i \right)\right)\Delta +\sum_i \left(\sum_j \left\lbrack f_{x|y} \left(x_i |y_j \right)f_x \left(y_j \right){\mathrm{log}}_2 f_{x|y} \left(x_i |x_j \right)\right\rbrack \cdot \Delta \right)\cdot \Delta$
'Information theory' 카테고리의 다른 글
| JPEG Compression - JPEG압축, DCT이산 코사인 변환 (1) | 2021.05.01 |
|---|---|
| Relative entropy, KL divergence (0) | 2021.04.25 |
| Lossy coding과 Entropy,Distortion (0) | 2021.04.24 |
| color space transform, chroma subsampling - 색공간 변환, 크로마 서브 샘플링 (0) | 2021.04.20 |
| Memoryless source, Markov source Entropy (0) | 2021.03.02 |



