JPEG는 (Lossy compression)손실이있는 압축 방법입니다. 즉, 본 raw 파일의 크기를 줄이기 위해 의도적으로 이미지를 손실합니다. 인간의 눈은 이미지의 전체 구조를 잃는 데 민감하지만 세부 정보에는 덜 민감합니다. 이미지의 전체 구조는 저주파 성분과 관련이 있고 세부 정보는 고주파 성분과 관련이 있습니다.
먼저 색 공간 변환이 필요합니다. Y 성분은 픽셀의 휘도를 나타내고 $C_b$ 및 $C_r$는 색상 정보를 나타냅니다.
인간의 눈은 색상 구성 요소보다 Luminance(밝기 정보)에 민감하므로 더 많은 색상 정보를 압축하고 Luminance(밝기) 정보를 유지해야합니다.
JPEG는 일반적으로 4 : 2 : 0 서브 샘플링 방법을 사용합니다. 4 : 2 : 0은 첫 번째 행에서 2 픽셀을 추출하고 두 번째 행에서 0 픽셀을 추출 함을 의미합니다. 이 방법을 사용하면 8 픽셀 중 2 픽셀을 추출하고 6 픽셀을 제거하여 크기를 줄일 수 있습니다.

그 유명한 Lenna 의 gray scale 사진(256 x 256) 을 이용하여 JPEG 압축을 진행해보겠습니다. 그레이 스케일은 색상이없는 흑백의 단색 음영 범위입니다. 각 픽셀에는 색상에 관계없이 lumninance(밝기 - brightness 또는 강도 - intensity) 값이 있습니다. 0의 intensity(검은 색)에서 최대 intensity(흰색)까지 그레이 스케일로 측정 할 수 있는데, 그레이 레벨 이미지는 이미지의 패턴과 속성을 분석하기에 충분합니다. 컬러 이미지를 사용하는 경우 각 계산 단계마다 3 (R, G, B) 시간을 수행해야합니다.
이산 코사인 변환 Discrete Cosine Transform :
이산 코사인 변환의 정확한 계산을 위해 이미지를로드 할 때 'double'을 사용해야합니다. 이미지 인코더가 평균이 0 인 이미지에서 작동하기 때문에, DCT를 적용하기 전에 양수 값과 음수 값을 모두 갖도록 평균 값을 제거하여 0 평균을 만들어야합니다.

DCT를 사용하면 주파수 영역에서 이미지를 분석 할 수 있습니다. JPEG 압축의 요점은 고주파 성분을 줄여 크기를 압축하는 것입니다. JPEG는 8x8 픽셀 블록을 기본 처리 단위로 사용합니다.
$B_{u,v} =\frac{1}{4}C_u C_v \sum_{x=0}^7 \sum_{y=0}^7 b_{x,y} \;\mathrm{cos}\frac{\left(2x+1\right)u\pi }{16}\mathrm{cos}\frac{\left(2y+1\right)v\pi }{16}$
$C_u =\left\lbrace \begin{array}{ll}\frac{1}{\sqrt{2}} & \mathrm{if}\;u=0\\1 & \mathrm{if}\;u\not= 0\end{array}\right.$
$b_{x,y} =\frac{1}{4}\sum_{u=0}^7 \sum_{v=0}^7 C_u C_v B_{u,v\;} \mathrm{cos}\frac{\left(2x+1\right)u\pi }{16}\mathrm{cos}\frac{\left(2y+1\right)v\pi }{16}$
아래 DTC result 사진은 Lenna 이미지에 DCT를 적용한 결과입니다. 그림의 크기는 256 x 256과 같은 값인 64 x 1024 = 65536이됩니다. 각 열은 크기가 8 x 8 인 한 블록의 DCT 결과를 나타냅니다. 각 행은 특정 주파수 값을 나타냅니다.
첫 번째 행에는 DC 값 정보가 포함되어 있으므로 대부분의 정보가 첫 번째 행에 저장되어 있음을 알 수 있습니다. 또한 그림의 9 행과 18 행에 작은 정보가 있음을 알 수 있습니다.

DCT 결과 한 블록의 첫 번째 열을 보면 첫 번째 행 값이 소위 DC 계수라고하는 가장 큰 값임을 알 수 있습니다. 앞에서 언급했듯이 DC 계수에는 블록의 기본 밝기를 결정하는 가장 중요한 정보가 있습니다. 다른 값은 고주파 성분과 관련된 AC 계수입니다.

첫번째 행를 선택하여 이미지를 나타내면, 다음과 같이 많은 정보가 첫째 행에 있는 것을 알 수 있습니다. 또한 distribution을 살펴 보면 DC계수의 값들이 비슷한 것을 알 수 있습니다.
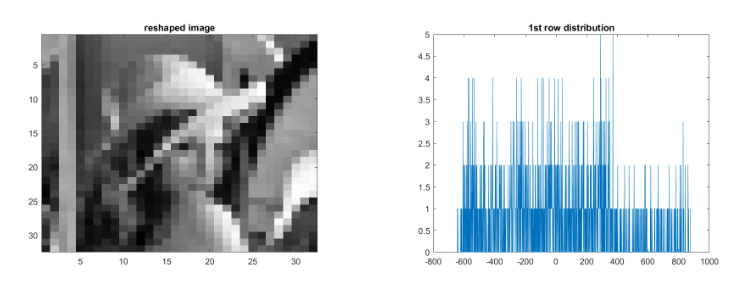
64번째 행의 이미지를 보면, high frequency 고주파 성분들로 구성되어 있으며, 많은 정보가 없는 것을 알 수 있습니다. distribution은 주로 0에 가깝게 밀집되어 위치합니다.

각 행의 variance of coefficient 대한 로그 sclae 결과 입니다.
아래 그림처럼, 매우 주기적으로 peak값을 볼 수 있는데, 이는 DCT 계산은 열 단위로 순차적으로 이루어지기 때문입니다. 첫 번째 선택은 DC 값이며 순차적으로 픽셀 번호 9 ($ AC_1_0 $), 18 ($ AC_2_0 $), 27 ($ AC_3_0 $)이 이어집니다. 두 번째 선택은 8 x 8 블록의 두 번째 열이며, 픽셀 번호 2 ($ AC_0_1 $), 19 ($ AC_1_1 $), 28 ($ AC_3_1 $) .. etc로 시퀀스를 볼 수 있습니다.


아래 그림은 log 스케일 coefficients of variance를 지그재그 스캔 결과입니다. 지그재그 스캔을 수행하면 분산이 가장 큰 계수를 함께 그룹화 할 수 있습니다. 또한 2 차원 계수를 1 차원 데이터 크기로 변환 할 수 있습니다. DC 값, 2 번째 픽셀 ($ AC_0_1 $), 9 번째 픽셀 ($ AC_1_0 $), 18 번째 픽셀 ($ AC_2_0 $), 10 번째 픽셀 ($AC_1_1$) 와 같이 zig zag 순서 로 정렬됩니다. ($AC_1_1 $ .. etc) .
양자화 Quantization :
양자화는 고주파 성분을 제거 할 수있는 방법입니다. 메인 아이디어는 각 계수를 양자화 행렬로 나누는 것입니다. DC 계수의 계수는 AC 계수의 값에 비해 매우 작다는 것을 알 수 있습니다. 값은 한 행에서 오른쪽으로 증가합니다. 그것은 더 높은 주파수를 의미하며 더 큰 값으로 나눕니다. 목표는 낮은 주파수에서 좋은 정밀도를 유지하고 높은 주파수 정보를 줄이는 것입니다.

양자화를 적용한 후 매트릭스에서 많은 0 값이 제거되어 고주파 성분이 제거되었음을 알 수 있습니다.

엔트로피 코딩 Entropy coding :
각 행의 엔트로피와 총 엔트로피를 계산해 보겠습니다.
아래 테이블에서 볼 수 있듯이 양자화 결과의 전체 행렬에 대한 엔트로피를 계산할 때 총 엔트로피는 거의 1입니다.이 값은 아무 것도 말해주지 않습니다. 이 값은 DC와 AC 계수의 조합이며 모든 행을 동일한 수준으로 고려하고 있습니다. DC 값의 첫 번째 행은 많은 값을 가질 수 있으므로 큰 엔트로피 (6.2960)가 발생합니다. 반면, 64 행 (고주파) 값은 거의 0에 가깝기 때문에 불확실성이 없다고 생각할 수 있습니다.

각 행의 Entropy 값을 계산해 Zig-zag 스캔을 통해 정렬해 볼 수 있습니다. 지그재그 순서로 20 번째 픽셀 값 ($ AC_4_1 $)까지 정보가 있지만 감소한 후 0으로 수렴합니다. 이는 대부분의 저주파 정보(DC component)가 양자화 후에도 유지된다는 것을 보여줍니다.
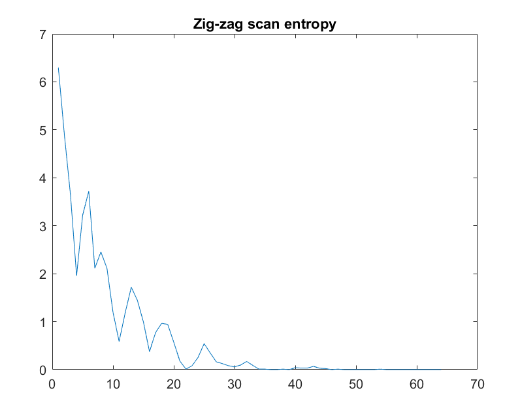
양자화 된 DC 값은 서로 매우 유사한 값을 갖습니다. 현재(Current) DC 계수와 이전 DC 계수의 차이을 계산하여 DC 정보를 줄일 수 있습니다. 값이 작을수록 비트 수가 적으며 DPCM (Differntial pulse code modulation)이라고 부릅니 다. 첫 번째 행 엔트로피를 계산하면 5.1008 으로 위의 Table 1 (6.2960)보다 감소한 것을 알 수 있습니다.

이미지 복구 Image reconstruction :
양자화 후 이미지 reconstruction은 다시 이전 값을 추가하여 DPCM의 결과에서 값을 재구성해야 합니다.
그 후, DCT 결과를 양자화 행렬로 나누었으므로 다시 곱하여 값을 복구합니다. 마지막으로 원본 이미지와 재구성 된 이미지의 차이를 계산하여 이미지의 품질을 평가할 수 있습니다. PSNR 값은 다음 식으로 구합니다.
${\mathrm{PSNR}}_{\left(\mathrm{dB}\right)} =10{\mathrm{log}}_{10} \frac{255\;x\;255}{\sigma_D^2 }$
아래 psnr 그래프 그림은 범위 [0.1,10]에서 $ \gamma$에 따른 PSNR (dB)의 값을 보여줍니다. $ \ gamma $가 클수록 PSNR (Peak Signal-to-noise ratio) 값이 작아 신호에 비해 많은 노이즈가 있음을 의미합니다. $ \ gamma $ 값이 작을수록 재구성 된 이미지의 품질이 더 좋아질 것이라고 추측 할 수 있습니다.
$ \ gamma $는 양자화 행렬을 곱하는 데 사용되며, $ \ gamma $가 많을수록 더 크고, 더 많은 양자화 행렬이 큰 값을 가지며 낮은 수준에 덜 민감합니다. 이는 양자화 된 파일에 더 많은 0을 만들고 코딩 할 정보를 줄이지 만 PSNR은 낮아져 이미지 품질이 저하됩니다.


'Information theory' 카테고리의 다른 글
| Relative entropy, KL divergence (0) | 2021.04.25 |
|---|---|
| Differential entropy (0) | 2021.04.24 |
| Lossy coding과 Entropy,Distortion (0) | 2021.04.24 |
| color space transform, chroma subsampling - 색공간 변환, 크로마 서브 샘플링 (0) | 2021.04.20 |
| Memoryless source, Markov source Entropy (0) | 2021.03.02 |



