Memoryless Source 란?
메모리성 기억성이 없는 이산적 모델로, 이산 무기억 소스(DMS), 이산 무기억 채널(DMC)라고 불립니다. 이 전 Symbol이 다음 Symbol과 연관이 없으며 독립적입니다. 예를들어, 'abracadabra'라는 텍스트가 있을 때 각각의 알파벳 letter의 확률이 독립적이라고 가정하고 계산할 수 있습니다.
Memoryless source의 Entropy를 구하는 MATLAB Function을 구현해보았습니다. Unique함수를 이용해 각각의 alphabet 빈도를 셀 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
function H = entropy(x)
%ENTROPY Compute entropy of the memoryless source x
% Compute the frequency of each symbol
alphabet = unique(x);
p = zeros(1, length(alphabet));
for i=1:length(alphabet)
p(i) = sum(x == alphabet(i));
end
% Get the probability
p = p/sum(p);
% Compute the entropy
H = -p*log2(p');
end
|
cs |
Markov source란?
Markov source는 이전의 Symbol이 그 다음 Symbol에도 영향을 미치는 것이 Memory less source와 다른 점입니다. 예를들어 1차 Markov source의 경우 이전의 Symbol와 다음 Symbol에 영향을 미치고, 2차인 경우 이전의 2가지 Symbol이 다음 Symbol에 영향을 미치게 됩니다.
따라서 Memoryless source보다 불확실성이 줄어들기에, Entropy가 낮은 특성을 지니고 있습니다.
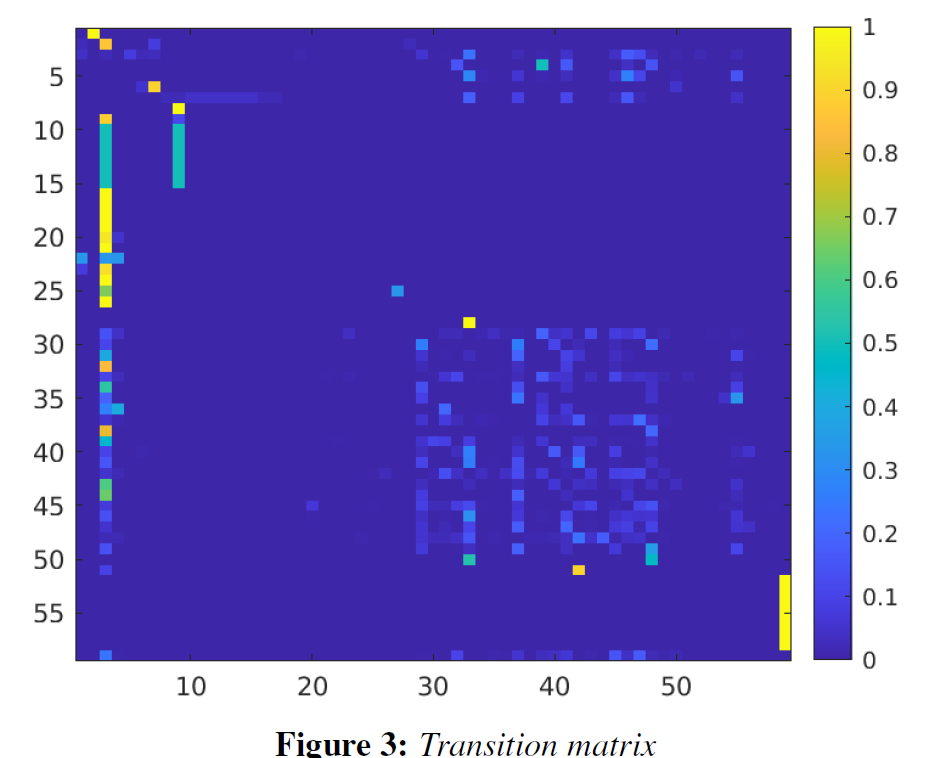
이전 예시와 같이 source 'abracadabra'가 있다고 할 때 Figure 1은 Transition matrix입니다. a다음 b가 오는 경우는 2가지, a다음 c가 오는 경우는 1가지 이런식으로 각각 알파벳 다음에 어떤 알파벳이 오는지에 대한 Matrix입니다.

Transition matrix의 'row' 의 확률의 합은 1이 되어야 하기에, Figure2와 같이 Normalization을 해줍니다.

이제 $\Pr(x_n=a_j,x_{n-1}=a_i)$ 에 대한 Entropy계산을 위해 아래 식을 이용합니다. $H\left(X_n |X_{n-1} \right)=\sum_{i,j} P_r \left(X_n =j,X_{n-1} =i\right){\log}_2 P_r \left(X_n =j|X_{n-1} =i\right)$
Chain rule을 적용하면 다음과 같습니다.
$\Pr(x_n=a_j,x_{n-1}=a_i) = \Pr(x_{n-1}=a_i)\Pr(x_n=a_j|x_{n-1}=a_i)$
최종적으로, Entropy는 다음과 같이 계산할 수 있습니다. $\odot$는 곱셈을 나타냅니다.
$H(X) = \sum_i\Pr(x_{n-1}=a_i)(-\text{P}\odot\log_2\text{P})$
imagesc 함수를 이용해 Markov source 에 대한 Transition matrix를 이미지로 얻을 수 있습니다. 노란색에 가까울 수록 높은 확률을 의미하며, 하단 바 어두운 파란색에 가까울 수록 낮은 확률을 의미합니다.
MATLAB으로 구현한 코드입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
function [P,H] = entropy1(x)
%ENTROPY1 Compute the entropy of a first order markov source
% Markov entropy
alphabet = unique(x);
% Compute the probability of each symbol
p = zeros(1, length(alphabet));
for i=1:length(alphabet)
p(i) = sum(x == alphabet(i));
end
% Get the probability
p = p/sum(p);
% Compute the frequency of the pair (j,i)
P = zeros(length(alphabet),length(alphabet));
for k=1:length(x)-1
i = find(x(k) == alphabet);
j = find(x(k+1) == alphabet);
P(j, i) = P(j, i) + 1;
end
% Get the conditional probability
for i=1:length(alphabet)
if (sum(P(i,:))) > 0
P(i,:) = P(i,:)/sum(P(i,:));
end
end
% Compute the entropy
aux = -P.*log2(P);
aux(isnan(aux))=0;
H = sum(p*aux);
|
cs |
'Information theory' 카테고리의 다른 글
| Differential entropy (0) | 2021.04.24 |
|---|---|
| Lossy coding과 Entropy,Distortion (0) | 2021.04.24 |
| color space transform, chroma subsampling - 색공간 변환, 크로마 서브 샘플링 (0) | 2021.04.20 |
| Midrise quantizer, Midtread quantizer (0) | 2021.02.27 |
| Entropy란? (0) | 2021.02.27 |


