※'통계 기반 머신러닝' Statistical Machine learning 수업을 듣고 정리한 포스팅입니다.※
1.The Laplace distribution 라플라스 분포
라플라스 분포는 double sided exponential 분포라고도 부르며, 두꺼운 꼬리를 가지고 있다. 라플라스 분포는 0에 더 밀집되어 있다.
확률 밀도 함수 pdf는 다음과 같이 정의된다 :
$\mathrm{Lap}\left(x|\mu ,b\right)\approx \frac{1}{2b}e^{-\frac{|x-\mu |}{b}}$
평균 : $\mathrm{mean}=\;\mu$
모드 : $\mu$
분산 : $\mathrm{var}\;=\;2b^2$
2.The gamma distribution 감마 분포
감마 분포는 $\alpha$번째 시간이 일어날 때 까지 걸리는 시간에 대한 연속 확률 분포로 총 $\alpha$번의 사건이 발생할 때 까지 걸린 시간에 대한 분포를 보인다.
확률 밀도 함수 pdf는 다음과 같이 정의된다 :
shape a>0이고, rate b>0일 때,
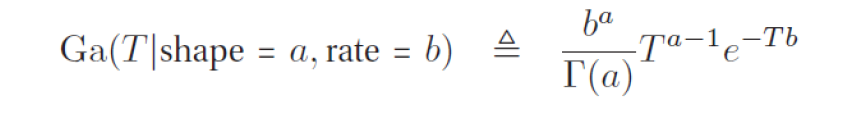
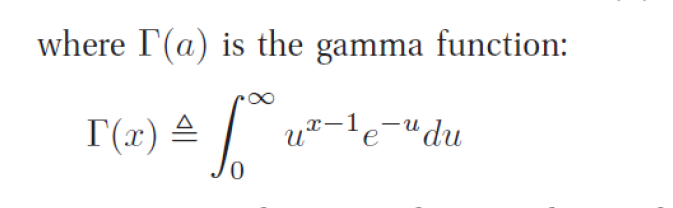
평균 : $\mathrm{mean}=\frac{a}{b}$
모드 : $\mathrm{mode}=\frac{\left(a-1\right)}{b}$
분산 : $\mathrm{var}=\frac{a}{b^2 }$
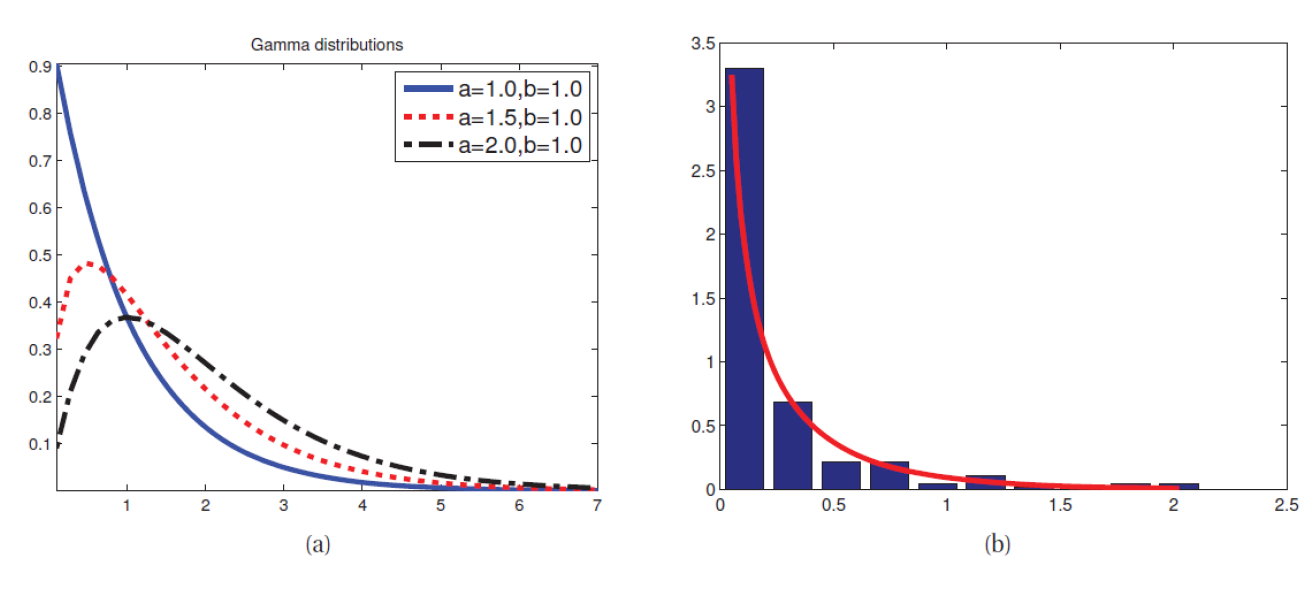
a가 양의 정수 값을 가질 때 얼랑 분포(Erlang distribution) 라고 하는데 감마 분포와 같다. 주로 많이 쓰이는 값은 a = 2로, 아래와 같다.
(포아송 분포에서 n번째 사건이 발생할 때 까지 걸리는 시간의 분포이다. n = 1일 때는 지수 분포와 같다.)
$\mathrm{Erlang}\left(x|\lambda \right)=\mathrm{Ga}\left(x|2,\lambda \right)$
얼랑 분포의 확률 밀도 함수(pdf는) 다음과 같이 정의된다 :
$f_x \left(x\right)=\frac{\lambda^n x^{n-1} e^{-\lambda x} }{\left(n-1\right)!}\;,\;\;\mathrm{when}\;x\ge 0,\mathrm{else0}$
평균 : $\mathrm{mean}=\frac{n}{\lambda }$
분산 : $\mathrm{var}=\frac{n}{\lambda^2 }$
3.Exponential distribution 지수 분포
어떤 사건이 발생할 때까지 경과 시간에 대한 연속 확률 분포로, 사건과 사건 사이의 경과된 시간에 대한 확률분포이다.
지수 분포는 감마 분포로부터 정의되며, 지수 형태의 모양을 가진다.
$\mathrm{Expon}\left(x|\lambda \right)\approx \mathrm{Ga}\left(x|1,\lambda \right),\lambda \;\mathrm{is}\;\mathrm{the}\;\mathrm{rate}\;\mathrm{parameter}$
확률 밀도 함수(pdf)는 다음과 같이 정의된다 :
$f_x \left(x\right)=\lambda e^{-x} \;\;\left(\mathrm{when}\;x\ge 0\right)\;\mathrm{else}\;0$
평균 : $\mathrm{mean}=\frac{1}{\lambda }$
분산 : $\mathrm{var}=\frac{1}{\lambda^2 }$
'Statistical Machine learning' 카테고리의 다른 글
| Statistical Machine learning 퀴즈 (0) | 2021.06.10 |
|---|---|
| [Statistical ML]Maximum Likelihood estimation (0) | 2021.04.18 |
| [Statistical ML]Hypothesis test 가설 검정 (0) | 2021.04.18 |
| [Statistical ML]Multivariate gaussian, central limit theorem (0) | 2021.04.18 |
| [Statistical ML]공분산(Covariance)과 상관계수(Correlation coefficient) (0) | 2021.04.18 |



