※'통계 기반 머신러닝' Statistical Machine learning 수업을 듣고 정리한 포스팅입니다.※
1.Statistical hypothesis test
Data는 어떤 의미를 가질 수 있도록 해석되어야 한다. 결과의 특정 구조를 가정하여 데이터를 해석할 수 있는데, 통계적 방법을 사용하여 가정( assumption)을 확인(confirm)하거나 기각(reject)할 수 있다. 이를 hypothesis(가설)이라고 하며 이를 위해 사용되는 통계 테스트를 통계적 가설 검정(statistical hypothesis test)라고 한다. 즉, 표본 통계랑에 의해 가설의 진위를 판정하는 방법이다.
Data distribution에 대한 주장을 하고 싶을 때, 머신 러닝이 적용된 한 결과의 집합이 다른 집합과 다르다면 우리는 통계적 가설 테스트에 의존해야 한다. 통계적 가설 검정은 데이터 샘플에 대한 답변을 정량화 하는데 중요하다.
통계적 추론 방식에는 크게 두가지가 있다.
|
1)검정 (Testing) 모집단의 특성에 의해 가설을 내세우고 모집단에서 추출한 표본 통계랑에 입각하여 기각하는 것을 의미한다. 보통 머신러닝에서 아래 두가지의 가정을 많이 쓴다. 2)추정 (Estimation) 표본으로부터 전체 모집단의 특정 모수에 대해 추정하는 것
|
Hypothesis test(가설 검정)은 항상 귀무 가설이 옳다는 전제하에서, 귀무가설의 확률 분포에서 검정 통계량의 결과가, 즉 귀무가설의 정당성이 의심스러운 범위에서 나타나는지 여부에 따라 귀무가설의 귀각/수용 여부를 결정한다.
Significance level(유의 수준) :
$\alpha$로 표기하며 귀무가설이 의심스러울 확률 수준으로, 귀무가설 확률 분포에서 발생할 가능성이 희박한 확률 수준(예 : 5%, 1%)
Confidence level :
1 - significant level로 관측된 표본 데이터에서 confidence 레벨을 나타낸다.
critical values(임계값) :
귀무가설의 기각 여부를 기준하는 경계값으로 유의 수준에 따라 결정되는 값이다.
유의 수준(5%,1%)라 할 때 그에 대응하는 확률 변수(변량)값이다.
P 값 :
귀무 가설에 대한 기각 기준으로 삼고, 관측되는 확률 값. 귀무 가설이 참이라는 가정 하에 얻어진 검정 통계량 값에 대응하여 구해진 확률로 귀무 가설을 얼마나 지지하는지 나타내는 확률이다.
$p-\mathrm{value}>\;\alpha$ : 귀무가설을 기각하는 데 실패 (not significant value)
$p-\mathrm{value}\le \;\alpha$ : 귀무 가설을 기각 (significant value)
귀무 가설이 타당하지 않음을 의미하며, $H_1$대립 가설이 오히려 타당함을 의미.
Null hypothesis($H_0$) 귀무가설, 공가설,영가설 :
검정의 대상으로 삼는 가설로, 귀무 가설이 옳은 것이라고 시작하고 가정한다.
귀무가설은 진실일 가능성이 적어 처음부터 기각될것이라고 예상하는 가설이다.
Significance level(유의 수준)에 따라 검정의 가정이 보류되고 거부되지 않는다.
First hypothesis ($H_1$) 대립가설 :
귀무가설에 대립되는 반대되는 가설로, 새로운 주장 또는 실제로 입증하고 싶은 가설이다.
Significance level(유의 수준)에 따라 검정의 가정이 보류되지 않고 거부된다.
예시) " Data가 표본 분포를 따른다 " 를 검증하고 싶을 때,
- 귀무가설($H_0$) : Data는 표본 분포를 따르지 않는다.
- 대립가설($H_1$) : Data는 표본 분포를 따른다.
- Significance level(유의 수준) : $\alpha$ = 5% (0.05) 로 귀무가설이 의심스러운 정도를 나타낸다.
- p-value : 귀무 가설을 지지하는 정도로 p-value가 0.07일 경우, $p\mathrm{value}\left(0\ldotp 07\right)>\;\alpha \left(0\ldotp 05\right)$ 로 귀무가설을 지지하는 정도가 귀무가설이 의심스러운 정도보다 높다. 따라서 이 경우 우리는 귀무 가설을 기각하는데 실패했다고 할 수 있다.
- confidence level = $1-\alpha =0\ldotp 95$
따라서 " Data가 표본 분포를 따른다 "라는 가설에 대하여, $95$%의 confidence level로 귀무가설을 기각하는데 실패했다고 할 수 있다.
기각(Reject)와 Failure to Reject(기각 실패)의 차이 :
먼저 p-value는 확률값이다. 이 뜻은 우리가 통계적 검증 결과를 해석하고 싶을 때 우리는 이것이 정확희 참(True)인지 거짓(False)인지 알 수가 없고 가능성에 대한 것만 알 수 있다.
귀무가설을 기각한다는 뜻은, 귀무가설의 가능성이 없어 보인다는 충분한 통계적 근거가 있음을을 의미한다.
귀무가설을 기각하지 않는다 것은, 귀무 가설을 기각할 충분한 통계적 증거가 없음을 의미한다.
귀무가설은 진실일 가능성이 적어 처음부터 기각될 것이라고 예상하는 가설이기에, 귀무가설을 accept(수용)한다는 단어를 쓰지 않고, 귀무가설을 "fail to reject"기각하는데 실패했다고 표현한다.
p-value의 해석 :
p value는 귀무가설이 옳고 그른지 나타내는 척도가 아니다.
$P_r \left(\mathrm{hypothesis}|\mathrm{data}\right)\to \mathrm{WRONG}$
$P_r \left(\mathrm{data}|\mathrm{hypothesis}\right)\to \mathrm{CORRECT}$
대신에 p-value는 사전에 통계적 검증에 기반한 주어진 데이터에 대한 확률로 생각할 수가 있다. 따라서 p-value는 data가 가설에 맞는지 아닌지에 대해 추론을 가능하게 해준다.
이 뜻은, 경험적 증거와 채택된 통계적 테스트에 기반하여 귀무가설을 기각하거나 기각하지 않기로 결정했음을 의미한다. 확률론적 주장으로만 제한되며 명확한 이진 True(참) 혹은 False(거짓)이 아니다.
critical values(임계값) 의 해석 :
어떤 검증(test)들은 p-value를 return하지 않는다. 대신, critical values(임계값)의 리스트들을 반환하는데, 이 값들은 통계 검증으로 Significance level(유의 수준)과 관련이 있다. 일반적으로 비모수 적이거나 분포가없는 통계 가설 검정이다. p-value를 return하거나 critical values를 return하는 결과는 비슷한 방식으로 해석된다. 임계값을 이용하여 해석할 때는 검증 통계값(test statistic)이 유의 수준(significance level)에 의해 채택된 임계값과 비교된다.
if test statistic < critical value : 귀무가설을 기각하지 않음
if teset statistic >= critical value : 귀무 가설을 기각함
통계 가설 검정의 해석은 확률적이며, 검사의 증거가 결과를 암시하고 그게 잘못될(mistaken) 수도 있음을 의미한다. 예를들어 작은 p값이 주어질 때(귀무 가설을 지지하는 정도가 낮음) 귀무가설이 거짓임을 의미하거나 사실이고 드물고 가능성이 낮은 사건이 관찰되었음을 의미할 수도 있다. 이런 오류를 False positive라고 부른다.
반대로, 큰 p값이 주어질 때(귀무 가설을 지지하는 정도가 크고 귀무가설을 기각하지 못함) 이는 귀무가설이 맞거나 혹은 귀무가설이 거짓이고 일부 예상치 못한 사건이 발생한 것일수도 있다. 이런 오류는 False negative라고 부른다.
이 두가지 Error을 Type I , Type II 에러라고 부른다.
- Type I ERROR : 참인 귀무 가설에 대해 잘못된 기각 혹은 False positive
- Type II ERROR : 거짓인 귀무 가설에 대한 잘못된 기각 혹은 False negative
따라서 이런 Error을 줄이기 위해 Significance level(유의 수준)을 잘 설정하는 것이 중요하다. 주로 많은 과학 분야에서 $\alpha$ 값으로 0.05, 0.01을 많이 사용한다. $\alpha$가 $3\cdot {10}^{-7}$ 인 경우에는 5-sigma라고 부르기도 한다. 이는 결과가 3.5 중 1의 확률로 우연에 기인했음을 의미하고, 이와 같은 임계값을 사용하기 위해서는 많은 양의 표본 샘플이 필요하다.
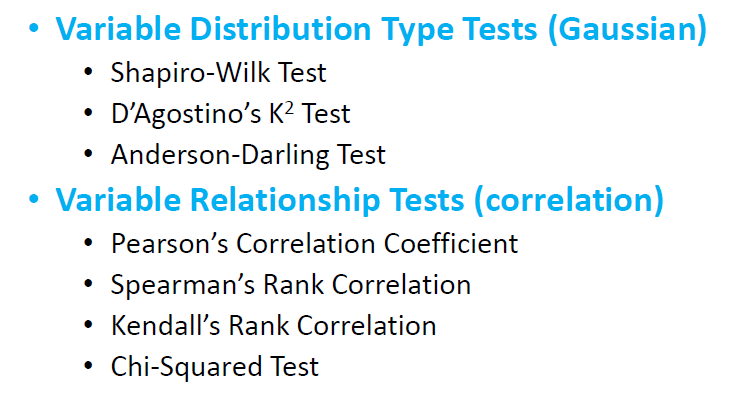
Hypothesis test의 종류 예시 :

'Statistical Machine learning' 카테고리의 다른 글
| [Statistical ML]라플라스 분포, 감마 분포 (0) | 2021.04.19 |
|---|---|
| [Statistical ML]Maximum Likelihood estimation (0) | 2021.04.18 |
| [Statistical ML]Multivariate gaussian, central limit theorem (0) | 2021.04.18 |
| [Statistical ML]공분산(Covariance)과 상관계수(Correlation coefficient) (0) | 2021.04.18 |
| [Statistical ML]Student t 분포 (0) | 2021.04.18 |



